Essays on Implied Spherical Space Forms in Statistics and Econometrics
Abstract
Rao (1945) pioneered the use of differential geometry in statistics by treating the Fisher information as a Riemannian metric. Its theoretical decedents, information geometers, Amari (1968), Costa et al. (2015), and Chen (2016), through explicit calculations, demonstrated the induced statistical manifolds have hyperbolic space forms. This manuscript opens an alternative line of geometric research and calls attention to the ubiquitous phenomena of implied spherical space forms in statistics, which act as benchmark manifolds for positive curvature bounds. By developing novel algebraico-topological techniques suitable to handle these manifolds intrinsically, it introduces significant improvements to two prominent, seemingly unrelated, statistical work:
- (a) For Andrews and Mikusheva (2016a,b), it provides a radically simplified proof and a succinct new theorem on the distance bound between a random vector and a manifold with a curvature bound;
- (b) For Huang et al. (1996); Kizhner et al. (2005), it offers rigorous definitions of related concepts and a new fundamental theory that allows smooth transforms between the Hilbert-Huang transform and the Fourier transform of a time series.
Through deep engagement with concrete statistical applications, it offers timely remarks about the methodological limitations of information geometry. In lieu of a grand synthesis unattainable at present, as empirical patches to the methodological wounds inflicted, it offers a suite of new interactive graphical tools based on the foregoing geometric discussions, in particular, the link between the spherical geometry and correlations, for the exploration of dynamic harmonic structures in high-dimensional time series.
Download
Excerpt
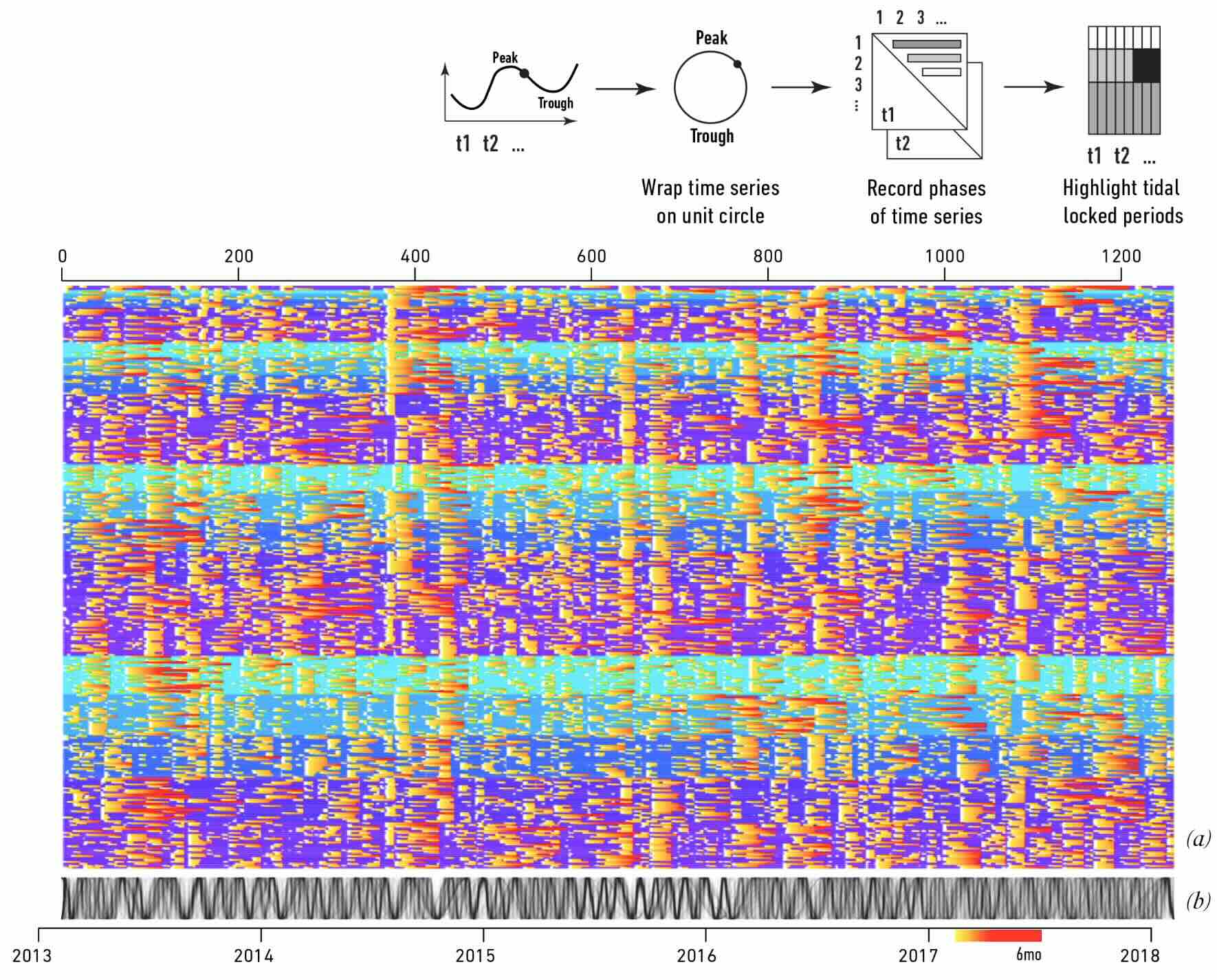 Prevalence and persistence of tidal locking in stock prices, 76.
Prevalence and persistence of tidal locking in stock prices, 76.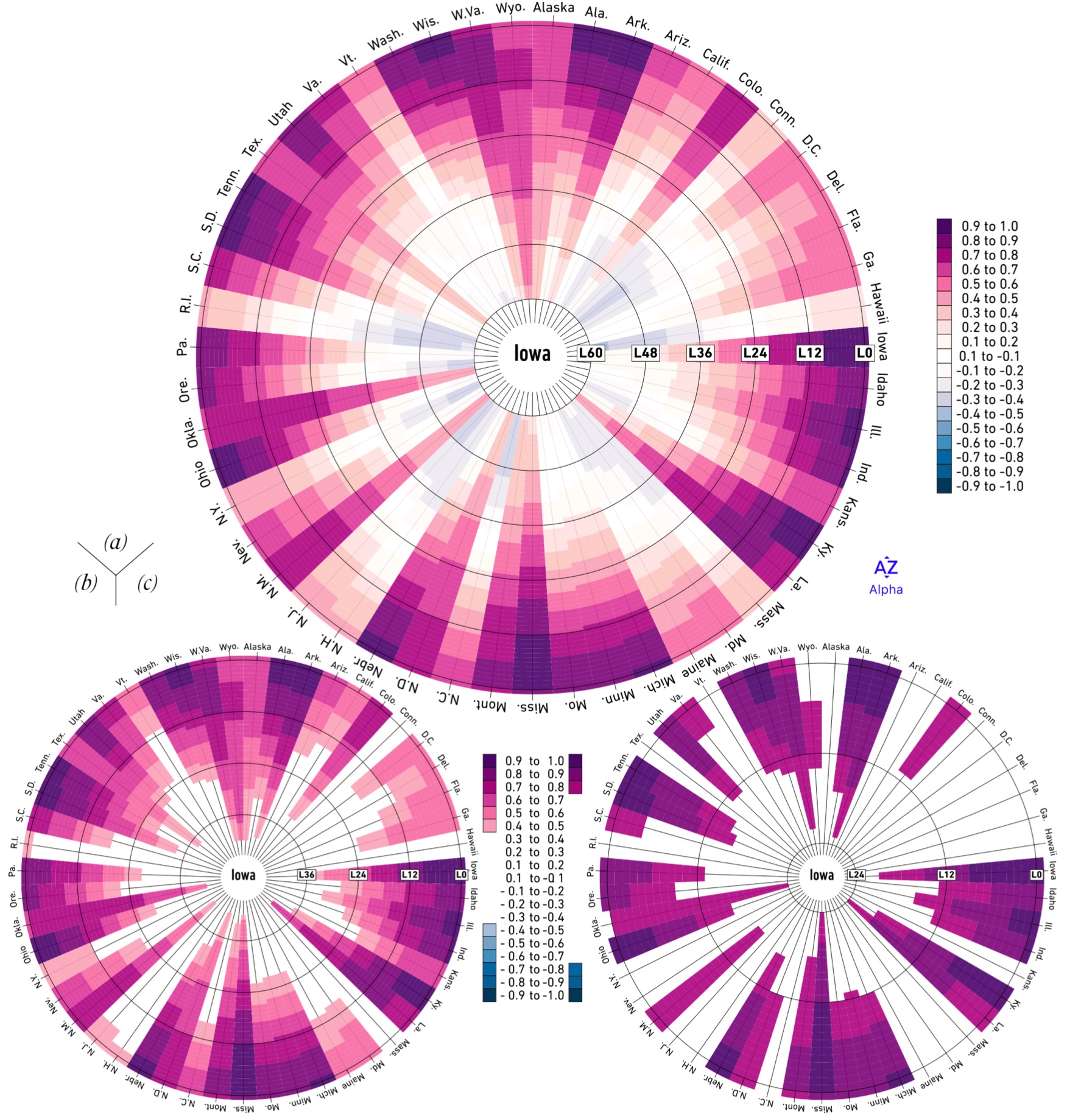 Adjusting tunnel plot correlation threshold, 113.
Adjusting tunnel plot correlation threshold, 113.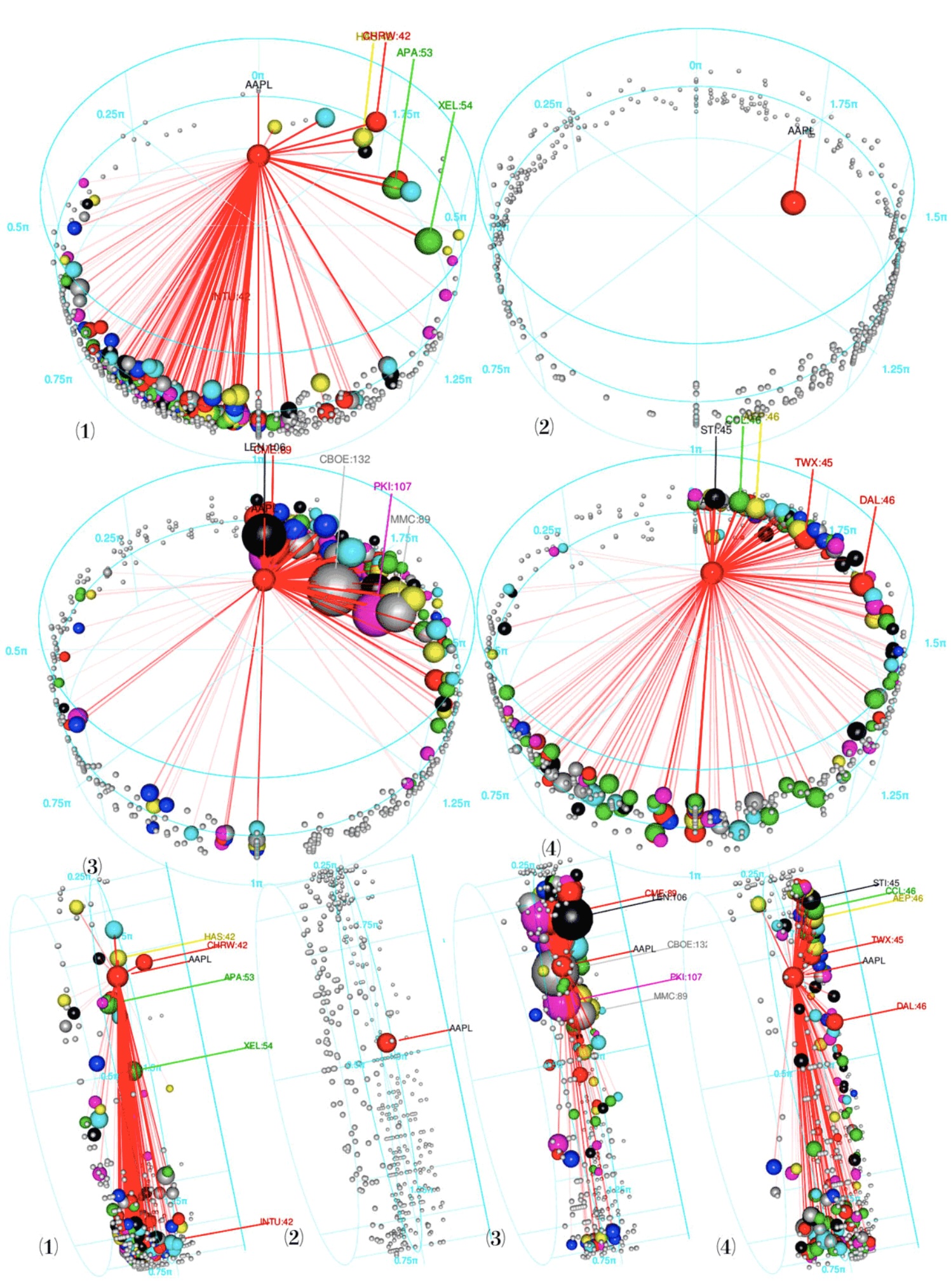 Closeup orbit plots of S&P stocks, 101.
Closeup orbit plots of S&P stocks, 101.